Answer below 👇
The winning move is Nf6! setting up the threat of Qxh6+ gxh6 Rh7#. Black can only fend this off with massive material sacrifices.
Everyone was blown away by the move, but several people noticed something interesting: some computers were struggling to find the move. For example, Stockfish running on the analysis board in lichess on my phone takes several seconds to figure it out.
This seems odd. While the line is very nice, it’s not very long or hard to understand. With one move, White sets up an unstoppable mate threat. It doesn’t even require any material sacrifices until mate is already assured. So why doesn’t the computer see it right away?
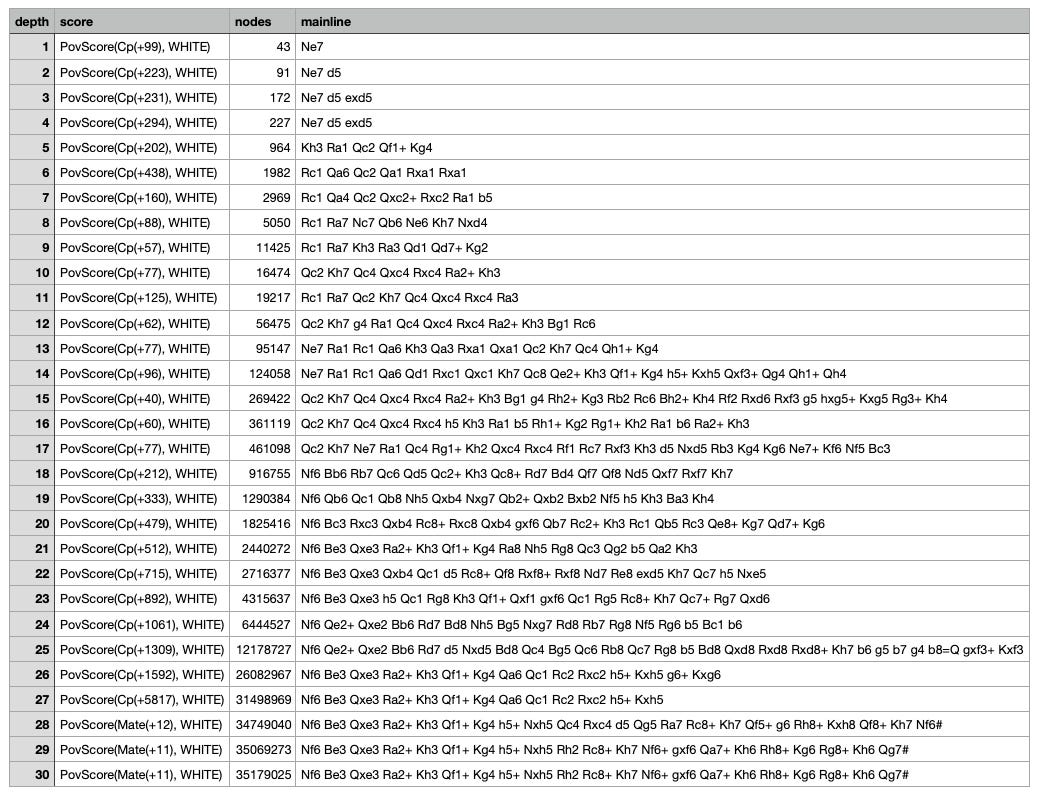
To get a better idea of what’s going on, I ran Stockfish at various depths:
Stockfish outputs its evaluation in centipawns, so to get the evaluation as it’s usually displayed in most interfaces you just divide by 100. An evaluation of +99 centipawns is .99 pawns.
Up to depth 17, Stockfish considers White to only have a slight advantage of less than one pawn. At 18 depth, the mainline starts with Nf6 and the evaluation jumps to +212, but curiously Stockfish still doesn’t see the mating combination. Black responds with an irrelevant move, Bb6, that doesn’t prevent mate, but White doesn’t follow up with Qxh6+!
At depth 21 Stockfish seems to have spotted the mate, because now Black responds with a series of desperation sacrifices to fend it off, starting with Be3. The evaluation adjusts to reflect a huge White advantage. Finally at depth 28 Stockfish announces mate in 12, which gets shortened to 11 at depth 29.
To understand what is going on here, we need to talk about how Stockfish actually works, and what it means by “depth”. Some may be surprised to learn that “depth 18” does not mean the engine has explored all combinations of 18 moves.
First of all, the number represents ply, not full “moves”. In traditional chess notation, a full move consists of a move for White and Black, like 1. e4 e5. In computer chess it’s more common to think in terms of ply, which is just a single move, like e4. Depth 18 means 18 ply (nine traditional “moves”).
More importantly though, the depth refers only to the depth of the mainline. It does not mean the computer has explored every possible combination of that length. To do so would be an enormous waste of resources, not to mention impossible. Even though Stockfish can calculate millions of moves per second, there are still far too many possibilities to calculate them all for more than a few moves.
White has 39 legal moves in the starting position, each of which lead to a similar number of possibilities for Black, resulting in a grand total of 1558 sequences. To get a sense of how many possibilities there are, let’s just print out every one move (two ply) sequence from the starting position.
Rc8+ Kh7 | Rc8+ Rxc8 | Rc8+ Qe8 | Rxg7 Kxg7 | Rxg7 Rg8 | Rxg7 Rf8 | Rxg7 Re8 | Rxg7 Rd8 | Rxg7 Rc8 | Rxg7 Rb8 | Rxg7 Ra7 | Rxg7 Ra6 | Rxg7 Ra5 | Rxg7 Ra4 | Rxg7 Ra3 | Rxg7 Ra2 | Rxg7 Ra1 | Rxg7 Qe8 | Rxg7 Qb8 | Rxg7 Qd7 | Rxg7 Qb7 | Rxg7 Qc6 | Rxg7 Qb6 | Rxg7 Qa6 | Rxg7 Qxd5 | Rxg7 Qc5 | Rxg7 Qa5 | Rxg7 Qc4 | Rxg7 Qxb4 | Rxg7 Qa4 | Rxg7 Qd3 | Rxg7 Qe2+ | Rxg7 Qf1+ | Rxg7 Ba7 | Rxg7 Bb6 | Rxg7 Bc5 | Rxg7 Be3 | Rxg7 Bc3 | Rxg7 Bf2 | Rxg7 Bb2 | Rxg7 Bg1 | Rxg7 Ba1 | Rxg7 h5 | Rf7 Kg8 | Rf7 Kh7 | Rf7 Rg8 | Rf7 Rf8 | Rf7 Re8 | Rf7 Rd8 | Rf7 Rc8 | Rf7 Rb8 | Rf7 Ra7 | Rf7 Ra6 | Rf7 Ra5 | Rf7 Ra4 | Rf7 Ra3 | Rf7 Ra2 | Rf7 Ra1 | Rf7 Qe8 | Rf7 Qb8 | Rf7 Qd7 | Rf7 Qb7 | Rf7 Qc6 | Rf7 Qb6 | Rf7 Qa6 | Rf7 Qxd5 | Rf7 Qc5 | Rf7 Qa5 | Rf7 Qc4 | Rf7 Qxb4 | Rf7 Qa4 | Rf7 Qd3 | Rf7 Qe2+ | Rf7 Qf1+ | Rf7 Ba7 | Rf7 Bb6 | Rf7 Bc5 | Rf7 Be3 | Rf7 Bc3 | Rf7 Bf2 | Rf7 Bb2 | Rf7 Bg1 | Rf7 Ba1 | Rf7 g6 | Rf7 h5 | Rf7 g5 | Re7 Kg8 | Re7 Kh7 | Re7 Rg8 | Re7 Rf8 | Re7 Re8 | Re7 Rd8 | Re7 Rc8 | Re7 Rb8 | Re7 Ra7 | Re7 Ra6 | Re7 Ra5 | Re7 Ra4 | Re7 Ra3 | Re7 Ra2 | Re7 Ra1 | Re7 Qe8 | Re7 Qb8 | Re7 Qd7 | Re7 Qb7 | Re7 Qc6 | Re7 Qb6 | Re7 Qa6 | Re7 Qxd5 | Re7 Qc5 | Re7 Qa5 | Re7 Qc4 | Re7 Qxb4 | Re7 Qa4 | Re7 Qd3 | Re7 Qe2+ | Re7 Qf1+ | Re7 Ba7 | Re7 Bb6 | Re7 Bc5 | Re7 Be3 | Re7 Bc3 | Re7 Bf2 | Re7 Bb2 | Re7 Bg1 | Re7 Ba1 | Re7 g6 | Re7 h5 | Re7 g5 | Rd7 Kg8 | Rd7 Kh7 | Rd7 Rg8 | Rd7 Rf8 | Rd7 Re8 | Rd7 Rd8 | Rd7 Rc8 | Rd7 Rb8 | Rd7 Ra7 | Rd7 Ra6 | Rd7 Ra5 | Rd7 Ra4 | Rd7 Ra3 | Rd7 Ra2 | Rd7 Ra1 | Rd7 Qb8 | Rd7 Qxd7 | Rd7 Qb7 | Rd7 Qc6 | Rd7 Qb6 | Rd7 Qa6 | Rd7 Qxd5 | Rd7 Qc5 | Rd7 Qa5 | Rd7 Qc4 | Rd7 Qxb4 | Rd7 Qa4 | Rd7 Qd3 | Rd7 Qe2+ | Rd7 Qf1+ | Rd7 Ba7 | Rd7 Bb6 | Rd7 Bc5 | Rd7 Be3 | Rd7 Bc3 | Rd7 Bf2 | Rd7 Bb2 | Rd7 Bg1 | Rd7 Ba1 | Rd7 g6 | Rd7 h5 | Rd7 g5 | Rb7 Kg8 | Rb7 Kh7 | Rb7 Rg8 | Rb7 Rf8 | Rb7 Re8 | Rb7 Rd8 | Rb7 Rc8 | Rb7 Rb8 | Rb7 Ra7 | Rb7 Ra6 | Rb7 Ra5 | Rb7 Ra4 | Rb7 Ra3 | Rb7 Ra2 | Rb7 Ra1 | Rb7 Qe8 | Rb7 Qd7 | Rb7 Qxb7 | Rb7 Qc6 | Rb7 Qb6 | Rb7 Qa6 | Rb7 Qxd5 | Rb7 Qc5 | Rb7 Qa5 | Rb7 Qc4 | Rb7 Qxb4 | Rb7 Qa4 | Rb7 Qd3 | Rb7 Qe2+ | Rb7 Qf1+ | Rb7 Ba7 | Rb7 Bb6 | Rb7 Bc5 | Rb7 Be3 | Rb7 Bc3 | Rb7 Bf2 | Rb7 Bb2 | Rb7 Bg1 | Rb7 Ba1 | Rb7 g6 | Rb7 h5 | Rb7 g5 | Ra7 Kg8 | Ra7 Kh7 | Ra7 Rg8 | Ra7 Rf8 | Ra7 Re8 | Ra7 Rd8 | Ra7 Rc8 | Ra7 Rb8 | Ra7 Rxa7 | Ra7 Qe8 | Ra7 Qb8 | Ra7 Qd7 | Ra7 Qb7 | Ra7 Qc6 | Ra7 Qb6 | Ra7 Qa6 | Ra7 Qxd5 | Ra7 Qc5 | Ra7 Qa5 | Ra7 Qc4 | Ra7 Qxb4 | Ra7 Qa4 | Ra7 Qd3 | Ra7 Qe2+ | Ra7 Qf1+ | Ra7 Bxa7 | Ra7 Bb6 | Ra7 Bc5 | Ra7 Be3 | Ra7 Bc3 | Ra7 Bf2 | Ra7 Bb2 | Ra7 Bg1 | Ra7 Ba1 | Ra7 g6 | Ra7 h5 | Ra7 g5 | Rc6 Kg8 | Rc6 Kh7 | Rc6 Rg8 | Rc6 Rf8 | Rc6 Re8 | Rc6 Rd8 | Rc6 Rc8 | Rc6 Rb8 | Rc6 Ra7 | Rc6 Ra6 | Rc6 Ra5 | Rc6 Ra4 | Rc6 Ra3 | Rc6 Ra2 | Rc6 Ra1 | Rc6 Qb8 | Rc6 Qb7 | Rc6 Qxc6 | Rc6 Qb6 | Rc6 Qa6 | Rc6 Qxd5 | Rc6 Qc5 | Rc6 Qa5 | Rc6 Qc4 | Rc6 Qxb4 | Rc6 Qa4 | Rc6 Qd3 | Rc6 Qe2+ | Rc6 Qf1+ | Rc6 Ba7 | Rc6 Bb6 | Rc6 Bc5 | Rc6 Be3 | Rc6 Bc3 | Rc6 Bf2 | Rc6 Bb2 | Rc6 Bg1 | Rc6 Ba1 | Rc6 g6 | Rc6 h5 | Rc6 g5 | Rc5 Kg8 | Rc5 Kh7 | Rc5 Rg8 | Rc5 Rf8 | Rc5 Re8 | Rc5 Rd8 | Rc5 Rc8 | Rc5 Rb8 | Rc5 Ra7 | Rc5 Ra6 | Rc5 Ra5 | Rc5 Ra4 | Rc5 Ra3 | Rc5 Ra2 | Rc5 Ra1 | Rc5 Qe8 | Rc5 Qb8 | Rc5 Qd7 | Rc5 Qb7 | Rc5 Qc6 | Rc5 Qb6 | Rc5 Qa6 | Rc5 Qxc5 | Rc5 Qa5 | Rc5 Qc4 | Rc5 Qxb4 | Rc5 Qa4 | Rc5 Qd3 | Rc5 Qe2+ | Rc5 Qf1+ | Rc5 Bxc5 | Rc5 Be3 | Rc5 Bc3 | Rc5 Bf2 | Rc5 Bb2 | Rc5 Bg1 | Rc5 Ba1 | Rc5 dxc5 | Rc5 g6 | Rc5 h5 | Rc5 g5 | Rc4 Kg8 | Rc4 Kh7 | Rc4 Rg8 | Rc4 Rf8 | Rc4 Re8 | Rc4 Rd8 | Rc4 Rc8 | Rc4 Rb8 | Rc4 Ra7 | Rc4 Ra6 | Rc4 Ra5 | Rc4 Ra4 | Rc4 Ra3 | Rc4 Ra2 | Rc4 Ra1 | Rc4 Qe8 | Rc4 Qb8 | Rc4 Qd7 | Rc4 Qb7 | Rc4 Qc6 | Rc4 Qb6 | Rc4 Qa6 | Rc4 Qxd5 | Rc4 Qc5 | Rc4 Qa5 | Rc4 Qxc4 | Rc4 Qxb4 | Rc4 Qa4 | Rc4 Ba7 | Rc4 Bb6 | Rc4 Bc5 | Rc4 Be3 | Rc4 Bc3 | Rc4 Bf2 | Rc4 Bb2 | Rc4 Bg1 | Rc4 Ba1 | Rc4 g6 | Rc4 h5 | Rc4 g5 | Rc3 Kg8 | Rc3 Kh7 | Rc3 Rg8 | Rc3 Rf8 | Rc3 Re8 | Rc3 Rd8 | Rc3 Rc8 | Rc3 Rb8 | Rc3 Ra7 | Rc3 Ra6 | Rc3 Ra5 | Rc3 Ra4 | Rc3 Ra3 | Rc3 Ra2 | Rc3 Ra1 | Rc3 Qe8 | Rc3 Qb8 | Rc3 Qd7 | Rc3 Qb7 | Rc3 Qc6 | Rc3 Qb6 | Rc3 Qa6 | Rc3 Qxd5 | Rc3 Qc5 | Rc3 Qa5 | Rc3 Qc4 | Rc3 Qxb4 | Rc3 Qa4 | Rc3 Qd3 | Rc3 Qe2+ | Rc3 Qf1+ | Rc3 Ba7 | Rc3 Bb6 | Rc3 Bc5 | Rc3 Be3 | Rc3 Bxc3 | Rc3 Bf2 | Rc3 Bg1 | Rc3 g6 | Rc3 h5 | Rc3 g5 | Rc2 Kg8 | Rc2 Kh7 | Rc2 Rg8 | Rc2 Rf8 | Rc2 Re8 | Rc2 Rd8 | Rc2 Rc8 | Rc2 Rb8 | Rc2 Ra7 | Rc2 Ra6 | Rc2 Ra5 | Rc2 Ra4 | Rc2 Ra3 | Rc2 Ra2 | Rc2 Ra1 | Rc2 Qe8 | Rc2 Qb8 | Rc2 Qd7 | Rc2 Qb7 | Rc2 Qc6 | Rc2 Qb6 | Rc2 Qa6 | Rc2 Qxd5 | Rc2 Qc5 | Rc2 Qa5 | Rc2 Qc4 | Rc2 Qxb4 | Rc2 Qa4 | Rc2 Qd3 | Rc2 Qe2+ | Rc2 Qf1+ | Rc2 Ba7 | Rc2 Bb6 | Rc2 Bc5 | Rc2 Be3 | Rc2 Bc3 | Rc2 Bf2 | Rc2 Bb2 | Rc2 Bg1 | Rc2 Ba1 | Rc2 g6 | Rc2 h5 | Rc2 g5 | Rc1 Kg8 | Rc1 Kh7 | Rc1 Rg8 | Rc1 Rf8 | Rc1 Re8 | Rc1 Rd8 | Rc1 Rc8 | Rc1 Rb8 | Rc1 Ra7 | Rc1 Ra6 | Rc1 Ra5 | Rc1 Ra4 | Rc1 Ra3 | Rc1 Ra2 | Rc1 Ra1 | Rc1 Qe8 | Rc1 Qb8 | Rc1 Qd7 | Rc1 Qb7 | Rc1 Qc6 | Rc1 Qb6 | Rc1 Qa6 | Rc1 Qxd5 | Rc1 Qc5 | Rc1 Qa5 | Rc1 Qc4 | Rc1 Qxb4 | Rc1 Qa4 | Rc1 Qd3 | Rc1 Qe2+ | Rc1 Qf1+ | Rc1 Ba7 | Rc1 Bb6 | Rc1 Bc5 | Rc1 Be3 | Rc1 Bc3 | Rc1 Bf2 | Rc1 Bb2 | Rc1 Bg1 | Rc1 Ba1 | Rc1 g6 | Rc1 h5 | Rc1 g5 | Ne7 Kh7 | Ne7 Rg8 | Ne7 Rf8 | Ne7 Re8 | Ne7 Rd8 | Ne7 Rc8 | Ne7 Rb8 | Ne7 Ra7 | Ne7 Ra6 | Ne7 Ra5 | Ne7 Ra4 | Ne7 Ra3 | Ne7 Ra2 | Ne7 Ra1 | Ne7 Qe8 | Ne7 Qb8 | Ne7 Qd7 | Ne7 Qb7 | Ne7 Qc6 | Ne7 Qb6 | Ne7 Qa6 | Ne7 Qd5 | Ne7 Qc5 | Ne7 Qa5 | Ne7 Qc4 | Ne7 Qxb4 | Ne7 Qa4 | Ne7 Qd3 | Ne7 Qe2+ | Ne7 Qf1+ | Ne7 Ba7 | Ne7 Bb6 | Ne7 Bc5 | Ne7 Be3 | Ne7 Bc3 | Ne7 Bf2 | Ne7 Bb2 | Ne7 Bg1 | Ne7 Ba1 | Ne7 g6 | Ne7 h5 | Ne7 d5 | Ne7 g5 | Nf6 Rg8 | Nf6 Rf8 | Nf6 Re8 | Nf6 Rd8 | Nf6 Rc8 | Nf6 Rb8 | Nf6 Ra7 | Nf6 Ra6 | Nf6 Ra5 | Nf6 Ra4 | Nf6 Ra3 | Nf6 Ra2 | Nf6 Ra1 | Nf6 Qe8 | Nf6 Qb8 | Nf6 Qd7 | Nf6 Qb7 | Nf6 Qc6 | Nf6 Qb6 | Nf6 Qa6 | Nf6 Qd5 | Nf6 Qc5 | Nf6 Qa5 | Nf6 Qc4 | Nf6 Qxb4 | Nf6 Qa4 | Nf6 Qd3 | Nf6 Qe2+ | Nf6 Qf1+ | Nf6 Ba7 | Nf6 Bb6 | Nf6 Bc5 | Nf6 Be3 | Nf6 Bc3 | Nf6 Bf2 | Nf6 Bb2 | Nf6 Bg1 | Nf6 Ba1 | Nf6 gxf6 | Nf6 g6 | Nf6 h5 | Nf6 d5 | Nf6 g5 | Nb6 Kg8 | Nb6 Kh7 | Nb6 Rg8 | Nb6 Rf8 | Nb6 Re8 | Nb6 Rd8 | Nb6 Rc8 | Nb6 Rb8 | Nb6 Ra7 | Nb6 Ra6 | Nb6 Ra5 | Nb6 Ra4 | Nb6 Ra3 | Nb6 Ra2 | Nb6 Ra1 | Nb6 Qe8 | Nb6 Qd7 | Nb6 Qc6 | Nb6 Qxb6 | Nb6 Qa6 | Nb6 Qd5 | Nb6 Qc5 | Nb6 Qa5 | Nb6 Qc4 | Nb6 Qxb4 | Nb6 Qa4 | Nb6 Qd3 | Nb6 Qe2+ | Nb6 Qf1+ | Nb6 Bxb6 | Nb6 Bc5 | Nb6 Be3 | Nb6 Bc3 | Nb6 Bf2 | Nb6 Bb2 | Nb6 Bg1 | Nb6 Ba1 | Nb6 g6 | Nb6 h5 | Nb6 d5 | Nb6 g5 | Nf4 Kg8 | Nf4 Kh7 | Nf4 Rg8 | Nf4 Rf8 | Nf4 Re8 | Nf4 Rd8 | Nf4 Rc8 | Nf4 Rb8 | Nf4 Ra7 | Nf4 Ra6 | Nf4 Ra5 | Nf4 Ra4 | Nf4 Ra3 | Nf4 Ra2 | Nf4 Ra1 | Nf4 Qe8 | Nf4 Qb8 | Nf4 Qd7 | Nf4 Qb7 | Nf4 Qc6 | Nf4 Qb6 | Nf4 Qa6 | Nf4 Qd5 | Nf4 Qc5 | Nf4 Qa5 | Nf4 Qc4 | Nf4 Qxb4 | Nf4 Qa4 | Nf4 Qd3 | Nf4 Qe2+ | Nf4 Qf1+ | Nf4 Ba7 | Nf4 Bb6 | Nf4 Bc5 | Nf4 Be3 | Nf4 Bc3 | Nf4 Bf2 | Nf4 Bb2 | Nf4 Bg1 | Nf4 Ba1 | Nf4 exf4 | Nf4 g6 | Nf4 h5 | Nf4 d5 | Nf4 g5 | Ne3 Kg8 | Ne3 Kh7 | Ne3 Rg8 | Ne3 Rf8 | Ne3 Re8 | Ne3 Rd8 | Ne3 Rc8 | Ne3 Rb8 | Ne3 Ra7 | Ne3 Ra6 | Ne3 Ra5 | Ne3 Ra4 | Ne3 Ra3 | Ne3 Ra2 | Ne3 Ra1 | Ne3 Qe8 | Ne3 Qb8 | Ne3 Qd7 | Ne3 Qb7 | Ne3 Qc6 | Ne3 Qb6 | Ne3 Qa6 | Ne3 Qd5 | Ne3 Qc5 | Ne3 Qa5 | Ne3 Qc4 | Ne3 Qxb4 | Ne3 Qa4 | Ne3 Qd3 | Ne3 Qe2+ | Ne3 Qf1+ | Ne3 Ba7 | Ne3 Bb6 | Ne3 Bc5 | Ne3 Bxe3 | Ne3 Bc3 | Ne3 Bb2 | Ne3 Ba1 | Ne3 g6 | Ne3 h5 | Ne3 d5 | Ne3 g5 | Nc3 Kg8 | Nc3 Kh7 | Nc3 Rg8 | Nc3 Rf8 | Nc3 Re8 | Nc3 Rd8 | Nc3 Rc8 | Nc3 Rb8 | Nc3 Ra7 | Nc3 Ra6 | Nc3 Ra5 | Nc3 Ra4 | Nc3 Ra3 | Nc3 Ra2 | Nc3 Ra1 | Nc3 Qe8 | Nc3 Qb8 | Nc3 Qd7 | Nc3 Qb7 | Nc3 Qc6 | Nc3 Qb6 | Nc3 Qa6 | Nc3 Qd5 | Nc3 Qc5 | Nc3 Qa5 | Nc3 Qc4 | Nc3 Qxb4 | Nc3 Qa4 | Nc3 Qd3 | Nc3 Qe2+ | Nc3 Qf1+ | Nc3 Ba7 | Nc3 Bb6 | Nc3 Bc5 | Nc3 Be3 | Nc3 Bxc3 | Nc3 Bf2 | Nc3 Bg1 | Nc3 g6 | Nc3 h5 | Nc3 d5 | Nc3 g5 | Kh3 Kg8 | Kh3 Kh7 | Kh3 Rg8 | Kh3 Rf8 | Kh3 Re8 | Kh3 Rd8 | Kh3 Rc8 | Kh3 Rb8 | Kh3 Ra7 | Kh3 Ra6 | Kh3 Ra5 | Kh3 Ra4 | Kh3 Ra3 | Kh3 Ra2 | Kh3 Ra1 | Kh3 Qe8 | Kh3 Qb8 | Kh3 Qd7+ | Kh3 Qb7 | Kh3 Qc6 | Kh3 Qb6 | Kh3 Qa6 | Kh3 Qxd5 | Kh3 Qc5 | Kh3 Qa5 | Kh3 Qc4 | Kh3 Qxb4 | Kh3 Qa4 | Kh3 Qd3 | Kh3 Qe2 | Kh3 Qf1+ | Kh3 Ba7 | Kh3 Bb6 | Kh3 Bc5 | Kh3 Be3 | Kh3 Bc3 | Kh3 Bf2 | Kh3 Bb2 | Kh3 Bg1 | Kh3 Ba1 | Kh3 g6 | Kh3 h5 | Kh3 g5 | Kh2 Kg8 | Kh2 Kh7 | Kh2 Rg8 | Kh2 Rf8 | Kh2 Re8 | Kh2 Rd8 | Kh2 Rc8 | Kh2 Rb8 | Kh2 Ra7 | Kh2 Ra6 | Kh2 Ra5 | Kh2 Ra4 | Kh2 Ra3 | Kh2 Ra2 | Kh2 Ra1 | Kh2 Qe8 | Kh2 Qb8 | Kh2 Qd7 | Kh2 Qb7 | Kh2 Qc6 | Kh2 Qb6 | Kh2 Qa6 | Kh2 Qxd5 | Kh2 Qc5 | Kh2 Qa5 | Kh2 Qc4 | Kh2 Qxb4 | Kh2 Qa4 | Kh2 Qd3 | Kh2 Qe2+ | Kh2 Qf1 | Kh2 Ba7 | Kh2 Bb6 | Kh2 Bc5 | Kh2 Be3 | Kh2 Bc3 | Kh2 Bf2 | Kh2 Bb2 | Kh2 Bg1+ | Kh2 Ba1 | Kh2 g6 | Kh2 h5 | Kh2 g5 | Kh1 Kg8 | Kh1 Kh7 | Kh1 Rg8 | Kh1 Rf8 | Kh1 Re8 | Kh1 Rd8 | Kh1 Rc8 | Kh1 Rb8 | Kh1 Ra7 | Kh1 Ra6 | Kh1 Ra5 | Kh1 Ra4 | Kh1 Ra3 | Kh1 Ra2 | Kh1 Ra1+ | Kh1 Qe8 | Kh1 Qb8 | Kh1 Qd7 | Kh1 Qb7 | Kh1 Qc6 | Kh1 Qb6 | Kh1 Qa6 | Kh1 Qxd5 | Kh1 Qc5 | Kh1 Qa5 | Kh1 Qc4 | Kh1 Qxb4 | Kh1 Qa4 | Kh1 Qd3 | Kh1 Qe2 | Kh1 Qf1+ | Kh1 Ba7 | Kh1 Bb6 | Kh1 Bc5 | Kh1 Be3 | Kh1 Bc3 | Kh1 Bf2 | Kh1 Bb2 | Kh1 Bg1 | Kh1 Ba1 | Kh1 g6 | Kh1 h5 | Kh1 g5 | Qxh6+ Kg8 | Qxh6+ gxh6| Qg5 Kg8 | Qg5 Kh7 | Qg5 Rg8 | Qg5 Rf8 | Qg5 Re8 | Qg5 Rd8 | Qg5 Rc8 | Qg5 Rb8 | Qg5 Ra7 | Qg5 Ra6 | Qg5 Ra5 | Qg5 Ra4 | Qg5 Ra3 | Qg5 Ra2+ | Qg5 Ra1 | Qg5 Qe8 | Qg5 Qb8 | Qg5 Qd7 | Qg5 Qb7 | Qg5 Qc6 | Qg5 Qb6 | Qg5 Qa6 | Qg5 Qxd5 | Qg5 Qc5 | Qg5 Qa5 | Qg5 Qc4 | Qg5 Qxb4 | Qg5 Qa4 | Qg5 Qd3 | Qg5 Qe2+ | Qg5 Qf1+ | Qg5 Ba7 | Qg5 Bb6 | Qg5 Bc5 | Qg5 Be3 | Qg5 Bc3 | Qg5 Bf2 | Qg5 Bb2 | Qg5 Bg1 | Qg5 Ba1 | Qg5 hxg5 | Qg5 g6 | Qg5 h5 | Qf4 Kg8 | Qf4 Kh7 | Qf4 Rg8 | Qf4 Rf8 | Qf4 Re8 | Qf4 Rd8 | Qf4 Rc8 | Qf4 Rb8 | Qf4 Ra7 | Qf4 Ra6 | Qf4 Ra5 | Qf4 Ra4 | Qf4 Ra3 | Qf4 Ra2+ | Qf4 Ra1 | Qf4 Qe8 | Qf4 Qb8 | Qf4 Qd7 | Qf4 Qb7 | Qf4 Qc6 | Qf4 Qb6 | Qf4 Qa6 | Qf4 Qxd5 | Qf4 Qc5 | Qf4 Qa5 | Qf4 Qc4 | Qf4 Qxb4 | Qf4 Qa4 | Qf4 Qd3 | Qf4 Qe2+ | Qf4 Qf1+ | Qf4 Ba7 | Qf4 Bb6 | Qf4 Bc5 | Qf4 Be3 | Qf4 Bc3 | Qf4 Bf2 | Qf4 Bb2 | Qf4 Bg1 | Qf4 Ba1 | Qf4 exf4 | Qf4 g6 | Qf4 h5 | Qf4 g5 | Qxd4 Kg8 | Qxd4 Kh7 | Qxd4 Rg8 | Qxd4 Rf8 | Qxd4 Re8 | Qxd4 Rd8 | Qxd4 Rc8 | Qxd4 Rb8 | Qxd4 Ra7 | Qxd4 Ra6 | Qxd4 Ra5 | Qxd4 Ra4 | Qxd4 Ra3 | Qxd4 Ra2+ | Qxd4 Ra1 | Qxd4 Qe8 | Qxd4 Qb8 | Qxd4 Qd7 | Qxd4 Qb7 | Qxd4 Qc6 | Qxd4 Qb6 | Qxd4 Qa6 | Qxd4 Qxd5 | Qxd4 Qc5 | Qxd4 Qa5 | Qxd4 Qc4 | Qxd4 Qxb4 | Qxd4 Qa4 | Qxd4 Qd3 | Qxd4 Qe2+ | Qxd4 Qf1+ | Qxd4 exd4 | Qxd4 g6 | Qxd4 h5 | Qxd4 g5 | Qe3 Kg8 | Qe3 Kh7 | Qe3 Rg8 | Qe3 Rf8 | Qe3 Re8 | Qe3 Rd8 | Qe3 Rc8 | Qe3 Rb8 | Qe3 Ra7 | Qe3 Ra6 | Qe3 Ra5 | Qe3 Ra4 | Qe3 Ra3 | Qe3 Ra2+ | Qe3 Ra1 | Qe3 Qe8 | Qe3 Qb8 | Qe3 Qd7 | Qe3 Qb7 | Qe3 Qc6 | Qe3 Qb6 | Qe3 Qa6 | Qe3 Qxd5 | Qe3 Qc5 | Qe3 Qa5 | Qe3 Qc4 | Qe3 Qxb4 | Qe3 Qa4 | Qe3 Qd3 | Qe3 Qe2+ | Qe3 Qf1+ | Qe3 Ba7 | Qe3 Bb6 | Qe3 Bc5 | Qe3 Bxe3 | Qe3 Bc3 | Qe3 Bb2 | Qe3 Ba1 | Qe3 g6 | Qe3 h5 | Qe3 g5 | Qd3 Kg8 | Qd3 Kh7 | Qd3 Rg8 | Qd3 Rf8 | Qd3 Re8 | Qd3 Rd8 | Qd3 Rc8 | Qd3 Rb8 | Qd3 Ra7 | Qd3 Ra6 | Qd3 Ra5 | Qd3 Ra4 | Qd3 Ra3 | Qd3 Ra2+ | Qd3 Ra1 | Qd3 Qe8 | Qd3 Qb8 | Qd3 Qd7 | Qd3 Qb7 | Qd3 Qc6 | Qd3 Qb6 | Qd3 Qa6 | Qd3 Qxd5 | Qd3 Qc5 | Qd3 Qa5 | Qd3 Qc4 | Qd3 Qxb4 | Qd3 Qa4 | Qd3 Qxd3 | Qd3 Ba7 | Qd3 Bb6 | Qd3 Bc5 | Qd3 Be3 | Qd3 Bc3 | Qd3 Bf2 | Qd3 Bb2 | Qd3 Bg1 | Qd3 Ba1 | Qd3 g6 | Qd3 h5 | Qd3 g5 | Qc3 Kg8 | Qc3 Kh7 | Qc3 Rg8 | Qc3 Rf8 | Qc3 Re8 | Qc3 Rd8 | Qc3 Rc8 | Qc3 Rb8 | Qc3 Ra7 | Qc3 Ra6 | Qc3 Ra5 | Qc3 Ra4 | Qc3 Ra3 | Qc3 Ra2+ | Qc3 Ra1 | Qc3 Qe8 | Qc3 Qb8 | Qc3 Qd7 | Qc3 Qb7 | Qc3 Qc6 | Qc3 Qb6 | Qc3 Qa6 | Qc3 Qxd5 | Qc3 Qc5 | Qc3 Qa5 | Qc3 Qc4 | Qc3 Qxb4 | Qc3 Qa4 | Qc3 Qd3 | Qc3 Qe2+ | Qc3 Qf1+ | Qc3 Ba7 | Qc3 Bb6 | Qc3 Bc5 | Qc3 Be3 | Qc3 Bxc3 | Qc3 Bf2 | Qc3 Bg1 | Qc3 g6 | Qc3 h5 | Qc3 g5 | Qf2 Kg8 | Qf2 Kh7 | Qf2 Rg8 | Qf2 Rf8 | Qf2 Re8 | Qf2 Rd8 | Qf2 Rc8 | Qf2 Rb8 | Qf2 Ra7 | Qf2 Ra6 | Qf2 Ra5 | Qf2 Ra4 | Qf2 Ra3 | Qf2 Ra2 | Qf2 Ra1 | Qf2 Qe8 | Qf2 Qb8 | Qf2 Qd7 | Qf2 Qb7 | Qf2 Qc6 | Qf2 Qb6 | Qf2 Qa6 | Qf2 Qxd5 | Qf2 Qc5 | Qf2 Qa5 | Qf2 Qc4 | Qf2 Qxb4 | Qf2 Qa4 | Qf2 Qd3 | Qf2 Qe2 | Qf2 Qf1+ | Qf2 Ba7 | Qf2 Bb6 | Qf2 Bc5 | Qf2 Be3 | Qf2 Bc3 | Qf2 Bxf2 | Qf2 Bb2 | Qf2 Ba1 | Qf2 g6 | Qf2 h5 | Qf2 g5 | Qe2 Kg8 | Qe2 Kh7 | Qe2 Rg8 | Qe2 Rf8 | Qe2 Re8 | Qe2 Rd8 | Qe2 Rc8 | Qe2 Rb8 | Qe2 Ra7 | Qe2 Ra6 | Qe2 Ra5 | Qe2 Ra4 | Qe2 Ra3 | Qe2 Ra2 | Qe2 Ra1 | Qe2 Qe8 | Qe2 Qb8 | Qe2 Qd7 | Qe2 Qb7 | Qe2 Qc6 | Qe2 Qb6 | Qe2 Qa6 | Qe2 Qxd5 | Qe2 Qc5 | Qe2 Qa5 | Qe2 Qc4 | Qe2 Qxb4 | Qe2 Qa4 | Qe2 Qd3 | Qe2 Qxe2+ | Qe2 Ba7 | Qe2 Bb6 | Qe2 Bc5 | Qe2 Be3 | Qe2 Bc3 | Qe2 Bf2 | Qe2 Bb2 | Qe2 Bg1 | Qe2 Ba1 | Qe2 g6 | Qe2 h5 | Qe2 g5 | Qc2 Kg8 | Qc2 Kh7 | Qc2 Rg8 | Qc2 Rf8 | Qc2 Re8 | Qc2 Rd8 | Qc2 Rc8 | Qc2 Rb8 | Qc2 Ra7 | Qc2 Ra6 | Qc2 Ra5 | Qc2 Ra4 | Qc2 Ra3 | Qc2 Ra2 | Qc2 Ra1 | Qc2 Qe8 | Qc2 Qb8 | Qc2 Qd7 | Qc2 Qb7 | Qc2 Qc6 | Qc2 Qb6 | Qc2 Qa6 | Qc2 Qxd5 | Qc2 Qc5 | Qc2 Qa5 | Qc2 Qc4 | Qc2 Qxb4 | Qc2 Qa4 | Qc2 Qd3 | Qc2 Qe2+ | Qc2 Qf1+ | Qc2 Ba7 | Qc2 Bb6 | Qc2 Bc5 | Qc2 Be3 | Qc2 Bc3 | Qc2 Bf2 | Qc2 Bb2 | Qc2 Bg1 | Qc2 Ba1 | Qc2 g6 | Qc2 h5 | Qc2 g5 | Qb2 Kg8 | Qb2 Kh7 | Qb2 Rg8 | Qb2 Rf8 | Qb2 Re8 | Qb2 Rd8 | Qb2 Rc8 | Qb2 Rb8 | Qb2 Ra7 | Qb2 Ra6 | Qb2 Ra5 | Qb2 Ra4 | Qb2 Ra3 | Qb2 Ra2 | Qb2 Ra1 | Qb2 Qe8 | Qb2 Qb8 | Qb2 Qd7 | Qb2 Qb7 | Qb2 Qc6 | Qb2 Qb6 | Qb2 Qa6 | Qb2 Qxd5 | Qb2 Qc5 | Qb2 Qa5 | Qb2 Qc4 | Qb2 Qxb4 | Qb2 Qa4 | Qb2 Qd3 | Qb2 Qe2+ | Qb2 Qf1+ | Qb2 Ba7 | Qb2 Bb6 | Qb2 Bc5 | Qb2 Be3 | Qb2 Bc3 | Qb2 Bf2 | Qb2 Bxb2 | Qb2 Bg1 | Qb2 g6 | Qb2 h5 | Qb2 g5 | Qa2 Kg8 | Qa2 Kh7 | Qa2 Rg8 | Qa2 Rf8 | Qa2 Re8 | Qa2 Rd8 | Qa2 Rc8 | Qa2 Rb8 | Qa2 Ra7 | Qa2 Ra6 | Qa2 Ra5 | Qa2 Ra4 | Qa2 Ra3 | Qa2 Rxa2+ | Qa2 Qe8 | Qa2 Qb8 | Qa2 Qd7 | Qa2 Qb7 | Qa2 Qc6 | Qa2 Qb6 | Qa2 Qa6 | Qa2 Qxd5 | Qa2 Qc5 | Qa2 Qa5 | Qa2 Qc4 | Qa2 Qxb4 | Qa2 Qa4 | Qa2 Qd3 | Qa2 Qe2+ | Qa2 Qf1+ | Qa2 Ba7 | Qa2 Bb6 | Qa2 Bc5 | Qa2 Be3 | Qa2 Bc3 | Qa2 Bf2 | Qa2 Bb2 | Qa2 Bg1 | Qa2 Ba1 | Qa2 g6 | Qa2 h5 | Qa2 g5 | Qe1 Kg8 | Qe1 Kh7 | Qe1 Rg8 | Qe1 Rf8 | Qe1 Re8 | Qe1 Rd8 | Qe1 Rc8 | Qe1 Rb8 | Qe1 Ra7 | Qe1 Ra6 | Qe1 Ra5 | Qe1 Ra4 | Qe1 Ra3 | Qe1 Ra2+ | Qe1 Ra1 | Qe1 Qe8 | Qe1 Qb8 | Qe1 Qd7 | Qe1 Qb7 | Qe1 Qc6 | Qe1 Qb6 | Qe1 Qa6 | Qe1 Qxd5 | Qe1 Qc5 | Qe1 Qa5 | Qe1 Qc4 | Qe1 Qxb4 | Qe1 Qa4 | Qe1 Qd3 | Qe1 Qe2+ | Qe1 Qf1+ | Qe1 Ba7 | Qe1 Bb6 | Qe1 Bc5 | Qe1 Be3 | Qe1 Bc3 | Qe1 Bf2 | Qe1 Bb2 | Qe1 Bg1 | Qe1 Ba1 | Qe1 g6 | Qe1 h5 | Qe1 g5 | Qd1 Kg8 | Qd1 Kh7 | Qd1 Rg8 | Qd1 Rf8 | Qd1 Re8 | Qd1 Rd8 | Qd1 Rc8 | Qd1 Rb8 | Qd1 Ra7 | Qd1 Ra6 | Qd1 Ra5 | Qd1 Ra4 | Qd1 Ra3 | Qd1 Ra2+ | Qd1 Ra1 | Qd1 Qe8 | Qd1 Qb8 | Qd1 Qd7 | Qd1 Qb7 | Qd1 Qc6 | Qd1 Qb6 | Qd1 Qa6 | Qd1 Qxd5 | Qd1 Qc5 | Qd1 Qa5 | Qd1 Qc4 | Qd1 Qxb4 | Qd1 Qa4 | Qd1 Qd3 | Qd1 Qe2+ | Qd1 Qf1+ | Qd1 Ba7 | Qd1 Bb6 | Qd1 Bc5 | Qd1 Be3 | Qd1 Bc3 | Qd1 Bf2 | Qd1 Bb2 | Qd1 Bg1 | Qd1 Ba1 | Qd1 g6 | Qd1 h5 | Qd1 g5 | Qc1 Kg8 | Qc1 Kh7 | Qc1 Rg8 | Qc1 Rf8 | Qc1 Re8 | Qc1 Rd8 | Qc1 Rc8 | Qc1 Rb8 | Qc1 Ra7 | Qc1 Ra6 | Qc1 Ra5 | Qc1 Ra4 | Qc1 Ra3 | Qc1 Ra2+ | Qc1 Ra1 | Qc1 Qe8 | Qc1 Qb8 | Qc1 Qd7 | Qc1 Qb7 | Qc1 Qc6 | Qc1 Qb6 | Qc1 Qa6 | Qc1 Qxd5 | Qc1 Qc5 | Qc1 Qa5 | Qc1 Qc4 | Qc1 Qxb4 | Qc1 Qa4 | Qc1 Qd3 | Qc1 Qe2+ | Qc1 Qf1+ | Qc1 Ba7 | Qc1 Bb6 | Qc1 Bc5 | Qc1 Be3 | Qc1 Bc3 | Qc1 Bf2 | Qc1 Bb2 | Qc1 Bg1 | Qc1 Ba1 | Qc1 g6 | Qc1 h5 | Qc1 g5 | g4 Kg8 | g4 Kh7 | g4 Rg8 | g4 Rf8 | g4 Re8 | g4 Rd8 | g4 Rc8 | g4 Rb8 | g4 Ra7 | g4 Ra6 | g4 Ra5 | g4 Ra4 | g4 Ra3 | g4 Ra2 | g4 Ra1 | g4 Qe8 | g4 Qb8 | g4 Qd7 | g4 Qb7 | g4 Qc6 | g4 Qb6 | g4 Qa6 | g4 Qxd5 | g4 Qc5 | g4 Qa5 | g4 Qc4 | g4 Qxb4 | g4 Qa4 | g4 Qd3 | g4 Qe2+ | g4 Qf1+ | g4 Ba7 | g4 Bb6 | g4 Bc5 | g4 Be3 | g4 Bc3 | g4 Bf2 | g4 Bb2 | g4 Bg1 | g4 Ba1 | g4 g6 | g4 h5 | g4 g5 | f4 Kg8 | f4 Kh7 | f4 Rg8 | f4 Rf8 | f4 Re8 | f4 Rd8 | f4 Rc8 | f4 Rb8 | f4 Ra7 | f4 Ra6 | f4 Ra5 | f4 Ra4 | f4 Ra3 | f4 Ra2 | f4 Ra1 | f4 Qe8 | f4 Qb8 | f4 Qd7 | f4 Qb7 | f4 Qc6 | f4 Qb6 | f4 Qa6 | f4 Qxd5 | f4 Qc5 | f4 Qa5 | f4 Qc4 | f4 Qxb4 | f4 Qa4 | f4 Qd3 | f4 Qe2+ | f4 Qf1+ | f4 Ba7 | f4 Bb6 | f4 Bc5 | f4 Be3 | f4 Bc3 | f4 Bf2 | f4 Bb2 | f4 Bg1 | f4 Ba1 | f4 exf4 | f4 g6 | f4 h5 | f4 g5In the table summarizing Stockfish’s analysis at different depths, the nodes increase quickly, but not nearly as quickly as the possibilities. The number of total possibilities increases by about a factor of around 40 at each depth, but the moves actually considered by Stockfish only increase by a factor of about two (with a lot of variation depending on other factors). For an analysis of any appreciable depth, Stockfish only looks at a tiny fraction of the possible sequences, far less than 1%.
The process by which Stockfish does this is known as pruning. As we’ve seen, it’s not feasible to search every possible continuation, even for computers, so Stockfish needs some way of focusing on the more promising continuations. To do this it relies on heuristics like not randomly giving away material. These generally work quite well, but occasionally cause it to miss the best move.
For example, consider the continuation Qd3 Qxd3 Rb7. White gives up a whole queen, then follows up with a rook nudge that accomplishes nothing. Clearly continuing to calculate this line would be pointless, since White’s play is going nowhere. But how do you tell “randomly giving away a queen” from “brilliant queen sacrifice?” The heuristics work most of the time, but not always.1
The answer to how computers make mistakes, in a single word, is pruning. That is, the best move is hidden somewhere in the vast tangle of moves not considered.
In answer to the question, “How many moves can you see ahead,” Capablanca is said to have responded, “I see only one move ahead, but it is always the correct one.” In this position, Stockfish seems to be doing the opposite: it sees many moves, but not the correct one. Apparently the prospect of hanging a knight, then a queen, causes it to abandon the line before seeing that it leads to mate. As you let it run longer, it increases both the depth and breadth of its search, until finally casting a wide enough net to see the winning continuation.
The challenge in understanding the limitations of engines is that our brains are not very good at understanding large numbers. At some point - perhaps somewhere between 1,000 and 1,000,000 - my brain starts to lump everything into a single category labeled “really big.” But of course, big numbers can differ just as much as small numbers. The number of moves a chess engine can see is unimaginably huge, but the possibilities in chess are unimaginably huger.
For a more detailed discussion of pruning and other limitations of engines, see Appendix 2, Advanced Engine Management, in Thinking Inside the Box by Jacob Aagaard.