How Elo Ratings Actually Work

Nobody is more obsessed with ratings than chess players. Other sports have ratings, but when it comes to bragging rights they take a back seat to tournaments or championships. The rating is seen for what it is: a statistical measure that’s useful for rankings and pairings, but isn’t the end-all be-all of competition. But in chess the rating is the essence of who you are as a player, even as a person.

Given how obsessed the chess world is with ratings, you’d think they’re somehow especially well-suited to chess. This turns out not to be the case. The association between Elo ratings and chess is largely a historical accident. The Elo system was created for chess, but it works just as well for any two player, zero-sum game.

In fact, in some ways the Elo system and chess are an awkward fit. Two unique features of chess are the advantage of the White pieces and the relatively high draw rate compared to other games. The Elo system doesn’t take color into account at all, even though we know White scores better at all levels. And it doesn’t predict how often draws will happen, just an expected score where a draw is worth half a win.

This week we’ll take a look under the hood of the Elo system. The hope is that by understanding how the rating system evolved and how it works (and where it fails) we’ll reduce its grip over us.

History

First of all, it’s Elo, not ELO. The name of the system isn’t an acronym, it’s a guy’s name. That guy is Arpad Elo, a physics professor and chess master who created the system in the 1960s. Other ratings systems already existed, but they didn’t work very well. What Elo did was to give the rating system solid grounding by basing it on statistics and probability theory.

The new system was announced in an article in the August 1967 issue of Chess Life. Readers were encouraged to mail in comments, but warned, “Please do not expect a personal reply, as correspondence on this subject will more than likely be too heavy to permit that courtesy.” Evidently, ratings were already a hot button issue!

Elo validated his system with several historical tests, including calculating the ratings of various high profile players over the course of their careers, which seemed to give plausible results for the relative strengths of the players.

How It Works

The rating system has two main components: prediction and updating. Prediction tells you the expected result when two players face off, given their ratings. Updating tells you how to adjust the players’ ratings after you find out the result of the game. These two parts are connected: if the system works, when a population of players competes over a period of time, the updates should produce ratings that lead to accurate predictions.

When tackling the prediction problem, the main issue Elo had to address was variability. In chess, the stronger player usually wins, but not always. The way Elo dealt with this was to see a chess game a lot like my nephew sees the Pokémon Trading Card Game.

Let me explain. My nephew has a large collection of Pokémon cards, but he isn’t old enough to read, let alone understand the intricate rules of Pokémon TCG, so he plays a simplified version that resembles the classic card game War. Each player flips the top card of their deck, and whoever turns over the Pokémon with higher hit points takes both cards.

Similarly, in Elo’s model a chess game is like both players drawing from a deck, and whoever draws the higher card wins. But the decks aren’t the same. The stronger player has higher cards, much like my nephew always seems to start with all the best Pokémon. In fact, he has one card that’s so powerful it’s actually made out of metal rather than card stock, and this card seems to find its way to the top of his deck in crucial situations. That last part has nothing to do with the Elo system, I’m just salty about it.

Getting back to Elo, his core assumption was that each player’s performance would form a normal distribution. In other words, if you’re a 1600 player, you’re drawing from a deck that mostly has cards around 1600, but there are a few 1400 and 1800 cards sprinkled in there too.

Normal distribution for a 1600 and 2000 player

The chance of one player winning is the chance that they will draw a higher card from their deck. In other words, the chance that the difference of their draws is positive (that’s just another way of saying the same thing).

An important point is that the system does not predict the likelihood of draws specifically, it just combines everything into an expected score where a draw is worth half a win. The expected score can be thought of as, “If these two players faced each other many times, how many points, on average, would each player expect to score per game?”

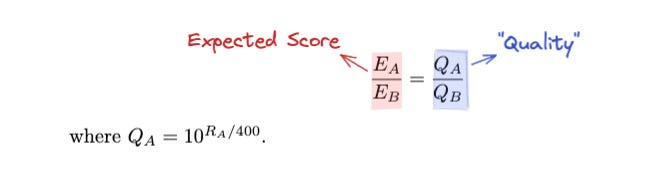
The formula for calculating the expected score is:

This is fairly mystifying, but there’s an alternative way of stating it that’s easier to understand and remember.

In this version we factor out a “quality” for each player based on their rating, which is the base 10 exponent of the rating divided by 400. Then the players’ expected points are proportional to their quality. 

You might wonder where the 10 and 400 come from in this formula. In fact, the same approach could work with other numbers, but Elo chose these parameters so that the numbers would roughly line up with the rating scale that players were already used to.

As it stands, a 400 point rating difference corresponds to 10 times greater expected points. This means when one player is 400 points higher rated, they are expected to score about 90%. (It’s only “about” 90% because it’s a ratio, not a percentage. A 400 point rating advantage translates into a 10:1 advantage in expected points. Converted to a fraction that’s 10 / (10 + 1) = 91%.) Similarly, a 200 point rating advantage implies about a 3:1 advantage in expected points, or close to 75%.

The process for updating the ratings after the game is relatively simple. It’s just the difference between the expected result and the actual result, scaled by a constant. In the Elo system this constant is called a k-value.

An example will make this more clear. Say we’ve got a 1683 going up against a 1732. Plugging the ratings into the formula, we find that the 1683 player is expected to score 43%. But you can’t score 43% in any single game, the only options are 0 (loss), ½ (draw), and 1 (win). Let’s say the 1683 player pulls off an upset and wins the game. The difference between the actual and expected score would then be 1 - 0.43 = 0.57. For a k-value of 24, the final rating adjustment would be 0.57 * 24 = 14.

Problems

The system turned out to work remarkably well. It’s been in continuous use by USCF since the 60s with minimal changes. FIDE soon adopted it as well, albeit with some changes in the implementation. Subsequently it spread well beyond chess to other applications. FIFA uses the Elo system for their world rankings. Even Tinder has used the Elo system to rank romantic partners (although they say they no longer do).

But it’s not perfect. There are several problems with the rating system. Many of these were laid out by Mark Glickman in A Comprehensive Guide to Chess Ratings.

• The system doesn’t take into account who has White and Black, even though White performs better at all rating levels.

• It doesn’t make any prediction about the expected draw rate, only the total score.

• It assumes every player has the same standard deviation. Thinking back to the deck of cards analogy, every player’s deck had the same distribution, just shifted higher or lower depending on their strength. But probably some players are more or less consistent than others.

• It only works within a given population of players. For that reason, if different populations of players are isolated, the ratings can get out of step. For example, it’s said that many players in India are currently underrated compared to the rest of the world.

There was a Kaggle competition to improve on the predictions of the Elo system. (Kaggle is a data science competition platform.) Basically, it’s not that hard to improve on the Elo predictions, but all the ways of doing so make the system more complicated. Some argue that the simplicity of the current system gives players more confidence that the ratings are being maintained fairly.

Ultimately, the rating system works quite well, all things considered. But these issues serve as a reminder that it’s just one system, based on a certain set of decisions and assumptions. All your abilities as a chess player can’t be captured by a single number, whether it’s an Elo rating or anything else.

Coping with Ratings

As Glickman observed:

One of the most important problems with the rating system has little to do with its computational aspects or the validity of its assumptions; it has to do with players’ perceptions of ratings, and the consequences of these perceptions. While the implementation of a chess rating system has increased the popularity of tournament chess, it may also be equally responsible for those who leave tournament chess.

Indeed, while raising your rating can be a powerful incentive to play, the fear of losing rating points can cause players to stop playing entirely. The lichess rating distribution graph even shows spikes at each increment of one hundred points, caused by players who stop playing when they hit a rating milestone.

The chess coach Dan Heisman has suggested that the USCF rating system should be based on classes, not ratings. The classes already exist, but they get less attention than ratings.

• 2200+ Master

• 2000-2199 Expert

• 1800-1999 Class A

• 1600-1799 Class B

• etc.

In Dan’s system, ratings would still be calculated behind the scenes, but only the classes would be published. This changes the incentives for playing a tournament. Currently, it’s just as easy to lose points as to gain them, so for those preoccupied with their ratings, tournaments are always a nerve wracking proposition. But class is based on your highest rating attained – you don’t lose it if your rating drops. In a system based on classes, you would never see your published rank go down. This means, in terms of ranking, playing a tournament is all upside: It’s the only way to level up, and you can never go down.

I think this is a great idea and in fact it’s similar to how many computer games do rankings. Unfortunately, chess players hate change and they love their ratings (even if it’s more of a love-hate thing). Realistically I don’t see ratings going away. That means we’re all on our own to navigate the ratings system as best we can.

Many years ago I posted a question on the poker forum 2+2 asking how often people looked at the balance of money in their online poker account. There was one answer I still think about all the time. This guy said he had an app that caused his screen to flash red whenever he was down for the session to alert him that he needed to make “bold, aggressive plays to get even.”

This was a joke (I think) but it’s pretty much how chess sites work by default. Rating is the chess version of account balance and your rating is plastered next to your name everywhere on the site. This is not helpful. Rating is an important measure of progress, but it’s not one you want to stare at continuously. Much like how in poker you cannot control if you win or lose any given hand, in chess you don’t directly control the short-term movements of your rating. It fluctuates based on how well your opponent plays, how unforeseen complications play out for you, and so on. In a perfect world you should look at your rating once every three months or so. On a day-to-day basis it’s much better to focus on things you can control like whether you’re sticking with your study plan, your level of focus during the game, and so on.

If you want to get closer to this ideal, you can take advantage of a setting lichess offers to turn off all ratings on the site. I started trying this about a week ago, and I have to say it’s made playing blitz online more enjoyable. Still, sometimes after a particularly intense game I still open my opponent’s profile in a new window and look at their rating. Just to see.