Centipawns Suck
Why the most popular chess metric makes no sense, and what we should use instead
If you want someone to believe something, tell them a number. If you really want them to believe it, tell them the number came from a computer. Most people are very trusting of numbers because they seem objective and scientific. But when you’re responsible for the numbers, you realize that they usually depend on a lot of assumptions and subjective choices. There’s no such thing as “just give me the data,” there are always decisions.
So I wasn’t too surprised that when I said on Twitter that the standard centipawn metric used to evaluate chess positions doesn’t make sense, it was people who work professionally with data who said, “Well yeah, duh, of course it makes no sense, everyone knows that.” But at the same time, the centipawn evaluation is the one number that seems to be displayed on every chess app from Lichess to Chess.com to Chessbase, and in general it seems to be taken quite seriously by chess players from beginners to grandmasters. So if it’s true that this number doesn’t make any sense, it’s hardly common knowledge.
It’s not that the centipawn evaluation is wrong. If the computer says one side is better, it’s almost always right. And if the number is bigger, it’s almost always right that that side is better by a bigger margin. The issue is with the metric itself. The scale of the numbers doesn’t make sense: it’s not connected to any discernible chess quantity. Supposedly 1 point = 1 pawn, but as we’ll see this doesn’t really hold up. Today we’ll go deeper into why centipawns don’t make sense and the alternative metric we should really use instead.
Centipawns
Let’s take a step back and talk about how computer evaluations work. Computers are known for calculating - grinding through possible moves - but you can rarely calculate every line to checkmate. At some point you have to stop calculating and evaluate the position. You need an evaluation function, which is something that takes the position as input, does some kind of math, and outputs a score representing who’s winning and by how much.
A natural starting point would be material since the pieces have well-known and accepted values.
This gets the material count for one side. You can do the same calculation for the other side and subtract them to get the material imbalance. Now you have an evaluation!
But pretty soon you realize this material evaluation is missing lots of important things about the position. Activity, king safety, pawn structure, space, and so on. So maybe you try to make your evaluation more nuanced. Let’s say you want to take into account piece mobility, so you count up the legal moves for both sides and add that to your material count. It works, the engine with the new evaluation beats the old one! But now your evaluation has drifted away from the idea of 1 point = 1 pawn, because you’re adding in this other number that has nothing to do with pawns.
Very broadly, this is how traditional engine evaluations work. They do a bunch of calculations with factors that seem relevant to evaluating a position, refined with trial and error to produce something that plays good chess. This approach works for creating a strong chess engine, but the results are difficult for humans to interpret. What we’ve done is taken a number the engine uses internally to perform calculations and used it as a metric for human consumption. The problem is that not only is the meaning of this number opaque, it often changes between different versions of the engine.
From the engine’s point of view, the evaluations are ultimately used to compare different positions, so as long as they are relatively correct - a better position produces a higher number - the size of the number doesn’t matter. You can always scale a metric by a constant: it makes no difference, for example, whether you express the evaluation in pawns (1 pawn = 1 point) or centipawns (1 pawn = 100 points). The problem is that whereas it’s easy to convert between pawns and centipawns (just multiply pawns by 100) there is no easy way to convert evaluations between different versions of Stockfish. You have a number that appears objective, but in fact floats around and isn’t tied to any definable real-world quantity.
Many commentators have pointed out that in recent versions, the evaluations seem to have gotten much bigger. For example, here’s a position I had in a tournament game. To me it looks like White is a pawn up and otherwise the position is unremarkable, but the engine gives an evaluation of +3.5. Okay, maybe White’s pieces are more active, but that still seems like a really big number! It’s hard to interpret evaluations like these in light of 1 point = 1 pawn.
I don’t doubt that Stockfish will win this position as White. In fact, some people attribute these growing numbers to Stockfish getting stronger and spotting more and more forcing wins in positions that appear to be only slightly better. This is probably part of the story, but there’s another part that’s much simpler: when you have a system that does a bunch of calculations and outputs a number, if you change the calculations, the number will change. The Stockfish team is primarily focused on making a stronger chess engine, so they try lots of changes and go with the version that performs the best. In the course of this process, maintaining a consistent evaluation that makes sense to humans is at best a secondary concern. It’s inevitable then that the evaluation will drift around as changes are made to the many parts of the process that produce the evaluation.
AlphaZero
Okay, hopefully I’ve convinced you about the problems with the centipawn evaluation. What’s the alternative?
Well we already have another kind of evaluation, one that makes much more sense. When DeepMind created AlphaZero, they built a completely different kind of chess engine from the ground up, including a completely different evaluation.
The AlphaZero approach to evaluation is fundamentally different from the approach used by old school engines like Stockfish. Rather than quantifying and adding up features of a chess position, it’s based on probabilities of outcomes. The scale goes from -1 to +1. -1 means certain Black victory, +1 certain White victory, and 0 a draw or equal chances for both sides.
Already we see some big differences from the centipawn evaluation. Whereas centipawns can come in weird, big numbers like 23, the AlphaZero evaluation is guaranteed to always be within the range -1 to 1. Additionally, those three big signposts at -1, 1, and 0 corresponding to the simple, real-world outcomes of win, loss, or draw, make it easy to interpret any other value. For example, -0.5 is halfway between a draw and a win for Black. Maybe it’s my poker background, but to me this approach makes far more sense.
Why didn’t chess engines use this approach from the beginning? The reason goes to the core of the difference between machine learning and traditional programming. In traditional programming, you write rules to produce the outcomes you want; old schools engines use a traditional programming approach. But in machine learning you start with the outcomes you want and have the computer teach itself the rules needed to get there. Everything flows backwards from the outcomes, so it makes sense that the evaluation would be based on that as well.
Regardless of how we got here, now that we have an evaluation that makes more sense and is easier to interpret, we should use it! Unfortunately, by the time neural network engines arrived, the chess world was already so used to centipawn evaluations that we bent over backwards to continue presenting everything in that format. Leela - the open source successor to AlphaZero - uses the AlphaZero-style evaluations internally, but converts them to the more familiar centipawn evaluations in most interfaces.
It’s possible to convert between the two systems. You do this by looking at a large number of games and fitting an equation to match the centipawn scores to outcomes. According to the Leela website, they use the formula
(Q is the AlphaZero style evaluation.) Using that equation to convert centipawns to Q looks like this:
Don’t worry too much if the details of the equation look confusing. The main point is that it’s non-linear, meaning that as the centipawn values get really big, that doesn’t translate at a steady rate into a greater chance of winning. For example, the difference between +0 and +3 is huge: it’s the difference between a dead equal and a winning position. But there’s little difference between a +6 and +9 position: they’re both completely winning. You can see this in the way the tails of the curve flatten out. Past a certain point, further increases in the centipawn evaluation make little difference to the chances of winning.
The Next Step
Great, we’ve gone from an evaluation that has no meaningful scale to one with a fixed range representing the probability of a White win or Black win. A natural next question would be, “The probability of winning for who?” The answer is, for the computer itself. Neither the centipawn nor AlphaZero-style evaluation factor in the possibility of human error. They’re both based entirely on the computer’s assessment of the best moves. As human chess players, what we’d really like is an evaluation that’s more relevant for our own chances.
While the current Leela evaluation doesn’t do this, it at least provides a framework for how it could be done. Given that -1 represents a Black win and +1 represents a White win, you could use the same scale to represent those probabilities in human games, you just need a way of simulating the human games. This could be done with something like Maia Chess, a different kind of neural network engine that imitates human play at varying levels.
It’s been just over 25 years since Deep Blue beat Garry Kasparov. On behalf of humans, I’d like to wave the white flag. Enough already, computers! You don’t have to get any stronger at chess! The most important next steps, both for chess players and for researchers who want to use chess to advance the state of AI, will not be marginal improvements in playing strength, but in the computer’s ability to express itself in a way that humans can understand and learn from.






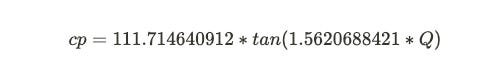

Great article. I thought a lot about this in grad school, where I used math models to predict dynamics of gene drives. I think even those working closely with the models tend to be overly trusting of the results, and I wrote a paper on the "reification" of these models. It was helpful to keep the humbling "all models are wrong, but some are useful" in mind.
For chess, I agree that the probability measure is at least more useful, and it seems similar to calculation for win probability based on difference in Elo ratings. I'm reminded of a completely closed position I once saw where there was no way to make progress, but the engines would give something like +2.0.
I wonder if Chess.com's Game Review uses the Q score, or some combination of Q and centipawns. I've noticed in a won position you can go from +9 to +6, and it will give you the thumbs up "good move" whereas anywhere else a -3 would be a blunder. Makes sense, since it makes little difference in winning probability when that far ahead.
Another confusing thing about the evaluation of the above position is despite stockfish evaluating white's advantage as "worth" three and a half pawns, if you actually try to give black say a bad knight or a bishop or two pawns, the evaluation will immediately swing in black's favor (any light squared bishop not immediately attacked will put the eval at -6 or so). I've heard tournament commentators for big events say stuff like "the engine thinks white's advantage is worth an extra rook" when the eval bar says +5, even though the evaluations don't work that way at all.